Golang program for implementation of AVL Trees
AVL trees are height balancing binary search tree. AVL tree checks the height of the left and the right sub-trees and assures that the difference is not more than 1. This difference is called the Balance Factor.
Example
package main
import (
"encoding/json"
"fmt"
)
type Key interface {
Less(Key) bool
Eq(Key) bool
}
type Node struct {
Data Key
Balance int
Link [2]*Node
}
func opp(dir int) int {
return 1 - dir
}
// single rotation
func single(root *Node, dir int) *Node {
save := root.Link[opp(dir)]
root.Link[opp(dir)] = save.Link[dir]
save.Link[dir] = root
return save
}
// double rotation
func double(root *Node, dir int) *Node {
save := root.Link[opp(dir)].Link[dir]
root.Link[opp(dir)].Link[dir] = save.Link[opp(dir)]
save.Link[opp(dir)] = root.Link[opp(dir)]
root.Link[opp(dir)] = save
save = root.Link[opp(dir)]
root.Link[opp(dir)] = save.Link[dir]
save.Link[dir] = root
return save
}
// adjust valance factors after double rotation
func adjustBalance(root *Node, dir, bal int) {
n := root.Link[dir]
nn := n.Link[opp(dir)]
switch nn.Balance {
case 0:
root.Balance = 0
n.Balance = 0
case bal:
root.Balance = -bal
n.Balance = 0
default:
root.Balance = 0
n.Balance = bal
}
nn.Balance = 0
}
func insertBalance(root *Node, dir int) *Node {
n := root.Link[dir]
bal := 2*dir - 1
if n.Balance == bal {
root.Balance = 0
n.Balance = 0
return single(root, opp(dir))
}
adjustBalance(root, dir, bal)
return double(root, opp(dir))
}
func insertR(root *Node, data Key) (*Node, bool) {
if root == nil {
return &Node{Data: data}, false
}
dir := 0
if root.Data.Less(data) {
dir = 1
}
var done bool
root.Link[dir], done = insertR(root.Link[dir], data)
if done {
return root, true
}
root.Balance += 2*dir - 1
switch root.Balance {
case 0:
return root, true
case 1, -1:
return root, false
}
return insertBalance(root, dir), true
}
// Insert a node into the AVL tree.
func Insert(tree **Node, data Key) {
*tree, _ = insertR(*tree, data)
}
// Remove a single item from an AVL tree.
func Remove(tree **Node, data Key) {
*tree, _ = removeR(*tree, data)
}
func removeBalance(root *Node, dir int) (*Node, bool) {
n := root.Link[opp(dir)]
bal := 2*dir - 1
switch n.Balance {
case -bal:
root.Balance = 0
n.Balance = 0
return single(root, dir), false
case bal:
adjustBalance(root, opp(dir), -bal)
return double(root, dir), false
}
root.Balance = -bal
n.Balance = bal
return single(root, dir), true
}
func removeR(root *Node, data Key) (*Node, bool) {
if root == nil {
return nil, false
}
if root.Data.Eq(data) {
switch {
case root.Link[0] == nil:
return root.Link[1], false
case root.Link[1] == nil:
return root.Link[0], false
}
heir := root.Link[0]
for heir.Link[1] != nil {
heir = heir.Link[1]
}
root.Data = heir.Data
data = heir.Data
}
dir := 0
if root.Data.Less(data) {
dir = 1
}
var done bool
root.Link[dir], done = removeR(root.Link[dir], data)
if done {
return root, true
}
root.Balance += 1 - 2*dir
switch root.Balance {
case 1, -1:
return root, true
case 0:
return root, false
}
return removeBalance(root, dir)
}
type intKey int
func (k intKey) Less(k2 Key) bool { return k < k2.(intKey) }
func (k intKey) Eq(k2 Key) bool { return k == k2.(intKey) }
func main() {
var tree *Node
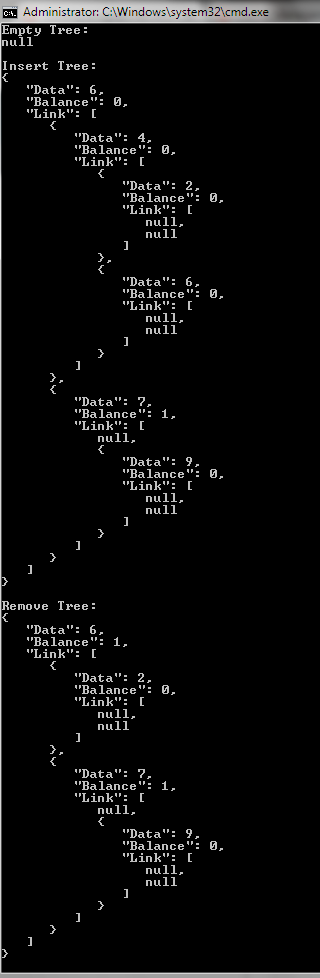
fmt.Println("Empty Tree:")
avl,_ := json.MarshalIndent(tree, "", " ")
fmt.Println(string(avl))
fmt.Println("\nInsert Tree:")
Insert(&tree, intKey(4))
Insert(&tree, intKey(2))
Insert(&tree, intKey(7))
Insert(&tree, intKey(6))
Insert(&tree, intKey(6))
Insert(&tree, intKey(9))
avl,_ = json.MarshalIndent(tree, "", " ")
fmt.Println(string(avl))
fmt.Println("\nRemove Tree:")
Remove(&tree, intKey(4))
Remove(&tree, intKey(6))
avl,_ = json.MarshalIndent(tree, "", " ")
fmt.Println(string(avl))
}
Refer: Data Structure and Algorithms - AVL Trees
