Cryptography
What is Cryptography?
The term "cryptography" is evolved from two Greek words, namely crypto and graphy. As per Greek language, crypto means secret and graphy means writing. The term crypto has become more popular with the introduction of all crypto currencies like Bitcoin, Ethereum, and Litecoin.
In simple terms, the process of altering messages in a way that their meaning is hidden from an enemy or opponent who might seize them, is known as Cryptography. Cryptography is the science of secret writing that brings numerous techniques to safeguard information that is present in an unreadable format. Only the designated recipients can be converted this unreadable format into the readable format.
In secure electronic transactions, cryptographic techniques are adopted to secure E-mail messages, credit card details, audio/video broadcasting, storage media and other sensitive information. By using cryptographic systems, the sender can first encrypt a message and then pass on it through the network. The receiver on the other hand can decrypt the message and restore its original content.
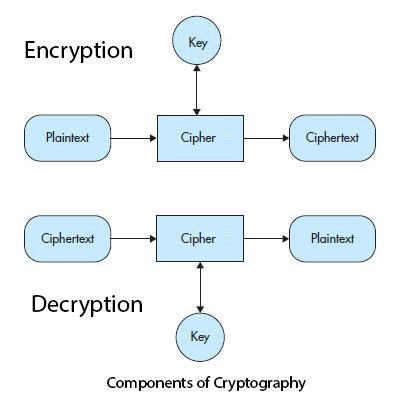
Components of Cryptography
Plaintext: Plaintext can be text, binary code, or an image that needs to be converted into a format that is unreadable by anybody except those who carry the secret to unlocking it. It refers to the original unencrypted or unadulterated message that the sender wishes to send.
Ciphertext: During the process of encryption plaintext get converted into a rushed format, the resulting format is called the ciphertext. It relates to the encrypted message, the receiver receives that. However, ciphertext is like the plaintext that has been operated on by the encryption process to reproduce a final output. This final output contains the original message though in a format, that is not retrievable unless official knows the correct means or can crack the code.
Encryption: Encryption, receives information and transforms it to an unreadable format that can be reversed. It is the process of encrypting the plaintext so it can provide the ciphertext. Encryption needs an algorithm called a cipher and a secret key. No one can decrypt the vital information on the encrypted message without knowing the secret key. Plaintext gets transformed into ciphertext using the encryption cipher.
Decryption: This is the reverse of the encryption process, in which it transforms the ciphertext back into the plaintext using a decryption algorithm and a secret key. In symmetric encryption, the key used to decrypt is the same as the key used to encrypt. On other hand, in asymmetric encryption or public-key encryption the key used to decrypt differs from the key used to encrypt.
Ciphers: The encryption and decryption algorithms are together known as ciphers. Perhaps the trickiest, interesting and most curious part in the encryption process is the algorithm or cipher. The algorithm or cipher is nothing more than a formula that comprises various steps that illustrate how the encryption/decryption process is being implemented on an information. A basic cipher takes bits and returns bits and it doesn't care whether bits represents textual information, an image, or a video.
Key: A key is generally a number or a set of numbers on which the cipher operates. In technical terms, a key is a discrete piece of information that is used to control the output (ciphertext and plaintext) of a given cryptographic algorithm. Encryption and decryption algorithms needs this key to encrypt or decrypt messages, respectively. Sender uses the encryption algorithm and the secret key to convert the plaintext into the ciphertext. On other hand receiver uses same decryption algorithm and the secret key to convert ciphertext back into the plaintext. The longer the secret key is, the harder it is for an attacker to decrypt the message.
Example of Cryptography (Classical Cipher)
Below is very basic example, we have created a simple cipher to encrypt and decrypt a plaintext into ciphertext and vice versa. The algorithm cipherAlgorithm() is same for encryption and decryption. The key, we have used is 01, 10 and 15 to encrypt and decrypt the message. The output of encryption is different each time when the key is different. This cipher shifts the letter based on key value, key plays an important role in cryptography.
Example
package main
import (
"fmt"
"unicode"
)
// Cipher encrypts and decrypts a string.
type Cipher interface {
Encryption(string) string
Decryption(string) string
}
// Cipher holds the key used to encrypts and decrypts messages.
type cipher []int
// cipherAlgorithm encodes a letter based on some function.
func (c cipher) cipherAlgorithm(letters string, shift func(int, int) int) string {
shiftedText := ""
for _, letter := range letters {
if !unicode.IsLetter(letter) {
continue
}
shiftDist := c[len(shiftedText)%len(c)]
s := shift(int(unicode.ToLower(letter)), shiftDist)
switch {
case s < 'a':
s += 'z' - 'a' + 1
case 'z' < s:
s -= 'z' - 'a' + 1
}
shiftedText += string(s)
}
return shiftedText
}
// Encryption encrypts a message.
func (c *cipher) Encryption(plainText string) string {
return c.cipherAlgorithm(plainText, func(a, b int) int { return a + b })
}
// Decryption decrypts a message.
func (c *cipher) Decryption(cipherText string) string {
return c.cipherAlgorithm(cipherText, func(a, b int) int { return a - b })
}
// NewCaesar creates a new Caesar shift cipher.
func NewCaesar(key int) Cipher {
return NewShift(key)
}
// NewShift creates a new Shift cipher.
func NewShift(shift int) Cipher {
if shift < -25 || 25 < shift || shift == 0 {
return nil
}
c := cipher([]int{shift})
return &c
}
func main() {
c := NewCaesar(1)
fmt.Println("Encrypt Key(01) abcd =>", c.Encryption("abcd"))
fmt.Println("Decrypt Key(01) bcde =>", c.Decryption("bcde"))
fmt.Println()
c = NewCaesar(10)
fmt.Println("Encrypt Key(10) abcd =>", c.Encryption("abcd"))
fmt.Println("Decrypt Key(10) klmn =>", c.Decryption("klmn"))
fmt.Println()
c = NewCaesar(15)
fmt.Println("Encrypt Key(15) abcd =>", c.Encryption("abcd"))
fmt.Println("Decrypt Key(15) pqrs =>", c.Decryption("pqrs"))
}
Output
Encrypt Key(01) abcd => bcde
Decrypt Key(01) bcde => abcd
Encrypt Key(10) abcd => klmn
Decrypt Key(10) klmn => abcd
Encrypt Key(15) abcd => pqrs
Decrypt Key(15) pqrs => abcd
Go provides extensive options for cryptography, such as encryption, hashing. Go have packages to support symmetric encryption algorithms: base64, AES and DES also.
What is Hashing?
The process of taking plaintext and transforms it into a digest of the plaintext information, in such a way that it is not intended to be decrypt is called Hashing. The output of Hashing is known as a hash, hash value, or message digest. Hashing is a intriguing area of cryptography and is different from encryption algorithms. Hashing creates a scrambled output that cannot be reversed easily. Technically, a hashing generates a fixed-length value that is relatively easy to compute in one direction, but nearly impossible to reverse.
Hashing Basics
A hash, hash value, or message digest is a value which is an output of plaintext or ciphertext being given into a hashing algorithm. No matter what is input into the hashing algorithm, the hash is of a fixed length and will always be of a certain length. The resulting hash has its length fixed by the design of the algorithm itself. We also refer, a hash as a summary of a file or message, often in numeric format. Hashes are being used in digital signatures, in the file and message authentication, and to protect the integrity of sensitive data.
A hash can take place into the category of a one-way function. This shows hash can compute when generated but difficult (or impossible) to compute in reverse. With a hash, initial computation is relatively easy to produce a condensed version of the message, but the original message should not be re-created from the hash.
Cryptographic Hash Functions
The simplest approach to hash a message is to slice it into chunks and process each chunk successively using a similar algorithm. This approach is called iterative hashing. Iterative hashing use a compression function that converts an input to a smaller output; and converts an input to an output of the same size, such that any two different inputs give two different outputs. Cryptographic hash functions are those hash functions which have a base on block ciphers. Examples of cryptographic hash functions include message digest (MD) algorithm based such as MD2, MD4 and MD5 and secure hash algorithm based (SHA) such as SHA-1, SHA-224, SHA-256, SHA-384 and SHA-512.
Message-Digest algorithm 5 (MD5)
This cryptographic hash algorithm developed by Ron Rivest in 1991. This algorithm takes a variable-length message as input and generates a fixed-length message digest of 128 bits. This algorithm uses Big-endian scheme where the least significant byte of a 32-bit word will be stored in the low-address byte position. This algorithm undergoes four rounds, each having 16 iterations, they use thus total 64 iterations. Hence it requires a 128-bit buffer. This is less secure but faster in operation as compared to SHA-1. This algorithm takes 2128 operations for detecting the original message from the given message digest and 264 operations to detect two messages generating the same message digest.
Secure Hash Algorithm (SHA-1)
This algorithm takes a variable-length message as input and generates a fixed-length message digest of 160 bits. This algorithm uses Little-endian scheme to interpret the message as a sequence of 32-bit words. In this algorithm, the most significant byte of a 32-bit word is stored in the low-address byte position. This algorithm undergoes four rounds, each having 20 iterations, they use thus total 80 iterations. Hence it requires a 160-bit buffer. This is more secure but slower in operation as compared to MD5. This algorithm takes 2160 operations for detecting the original message from the given message digest and 280 operations to detect two messages generating the same message digest.
Example
package main
import (
"crypto/md5"
"crypto/sha1"
"crypto/sha256"
"crypto/sha512"
"fmt"
)
func main() {
fmt.Println("\n----------------Small Message----------------\n")
message := []byte("Today web engineering has modern apps adhere to what is known as a single-page app (SPA) model.")
fmt.Printf("Md5: %x\n\n", md5.Sum(message))
fmt.Printf("Sha1: %x\n\n", sha1.Sum(message))
fmt.Printf("Sha256: %x\n\n", sha256.Sum256(message))
fmt.Printf("Sha512: %x\n\n", sha512.Sum512(message))
fmt.Println("\n\n----------------Large Message----------------\n")
message = []byte("Today web engineering has modern apps adhere to what is known as a single-page app (SPA) model. This model gives you an experience in which you never navigate to particular pages or even reload a page. It loads and unloads the various views of our app into the same page itself. If you've ever run popular web apps like Gmail, Facebook, Instagram, or Twitter, you've used a single-page app. In all those apps, the content gets dynamically displayed without requiring you to refresh or navigate to a different page. React gives you a powerful subjective model to work with and supports you to build user interfaces in a declarative and component-driven way.")
fmt.Printf("Md5: %x\n\n", md5.Sum(message))
fmt.Printf("Sha1: %x\n\n", sha1.Sum(message))
fmt.Printf("Sha256: %x\n\n", sha256.Sum256(message))
fmt.Printf("Sha512: %x\n\n", sha512.Sum512(message))
}
Output
----------------Small Message----------------
Md5: d53c7002ebeeaa872f02efdda82f76f0
Sha1: b56fd6c3eabc1ea6e880ffb7762d31a4b39bbcc9
Sha256: 0e81731d26a2ffd898be00c40bf0ab3c24ec82a0837311701193dd861efdb944
Sha512: 97be88309470c98e8ff840a74567c3948263251f3ac6f232a6e228cebc6daa6d95569a96
6a5f2ba5d694dc644d02c144849e7a181a159b583a2060e2ce3ad375
----------------Large Message----------------
Md5: f52c27fb5fa09afbb717e5ded9ef5707
Sha1: 86b1102f10518ef02089742862695e132ca6b5fe
Sha256: 88c9eca72b7b635458945710d12f6709af44dd02c0a3bb9b16c7e352b6d13f84
Sha512: 5400f78f1642d5b7df7a0c60e22e95ba04a94d16d33d008fc78a5002958f853ecc469bb8
786632c0be47a0c5b44d5f78aa9878abe7f00b688d8712c921aa81b8
Due to vulnerabilities in MD5 and SHA-1, some agencies has started using SHA-2 as early as 2011. SHA-2 is more secure, and it has a 256-bit and 512-bit block sizes. A common hash used on the Internet is SHA-2, SHA-1 is now deprecated and should be replaced if it's in use.
We commonly using this hash functions in public-key encryption, message authentication, key agreement protocols, digital signatures, integrity verification, identification protection and many other cryptographic contacts. Always there is a hash function somewhere under the hood whether we're encrypting an email, sending a message on your mobile phone, connecting to a HTTPS website, or connecting to a remote machine through IPSec or SSH.
List of real world examples where we are using Hash functions:
- Cloud storage systems use hash functions to analyze identical files and to find changed files.
- Git revision control system uses hash functions to detect files in a repository.
- Bitcoin using a hash function in its proof-of-work systems.
- Forensic analysts use hash values to verify that digital artifacts hasn't altered.
- NIDS use hashes to analyze known-malicious data going through a network.
Hash-based MAC (HMAC)
Hash-based MACs (HMACs) takes a long message as the input and produce a fixed-length output. In this scheme, the sender signs a message using the MAC and the receiver verifies it using the shared key. It hashes the key with the message using either of the two methods known as a secret prefix (key comes first and the message comes afterwards) or the secret suffix (key comes after the message).
High-level design of HMAC
Message Authentication Code (MAC) is a small part of information or a small algorithm, basically used to authenticate a message and to maintain integrity and authenticity assurances on the message. Hash-based Message Authentication Code is a message authentication code derived from a cryptographic hash function such as MD5 and SHA-1. The basic idea behind HMAC is to add a layer using a secret key in the existing message digest algorithms. Even if an attacker got the database of hashed passwords with the salts, they would still have a difficult time cracking them without the secret key. As algorithms such as MD5 and SHA-1 do not rely on the secret key, HMAC has been selected as mandatory-to-implement MAC for IP security. HMAC can work with any existing message digest algorithms (hash functions). It considers the message digest produced by the embedded hash function as a black box. It then uses the shared symmetric key to encrypt the message digest, thus, producing the final output, that is, MAC. HMAC is a calculation of a MAC through the use of a cryptographic hash function such as MD5 or SHA-1.
When we use SHA-1, then corresponding MAC would be known as HMAC-SHA1, or if SHA-2 is being used then we would say HMAC-SHA256. It is a good practice to store secret key in a separate location such as an environment variable rather than in the database with hashed passwords and salts.
Example
package main
import (
"crypto/hmac"
"crypto/rand"
"crypto/sha256"
"crypto/sha512"
"encoding/base64"
"fmt"
"io"
)
var secretKey = "4234kxzjcjj3nxnxbcvsjfj"
// Generate a salt string with 16 bytes of crypto/rand data.
func generateSalt() string {
randomBytes := make([]byte, 16)
_, err := rand.Read(randomBytes)
if err != nil {
return ""
}
return base64.URLEncoding.EncodeToString(randomBytes)
}
func main() {
message := "Today web engineering has modern apps adhere to what is known as a single-page app (SPA) model."
salt := generateSalt()
fmt.Println("Message: " + message)
fmt.Println("\nSalt: " + salt)
hash := hmac.New(sha256.New, []byte(secretKey))
io.WriteString(hash, message+salt)
fmt.Printf("\nHMAC-Sha256: %x", hash.Sum(nil))
hash = hmac.New(sha512.New, []byte(secretKey))
io.WriteString(hash, message+salt)
fmt.Printf("\n\nHMAC-sha512: %x", hash.Sum(nil))
}
Output
Message: Today web engineering has modern apps adhere to what is known as a sing
le-page app (SPA) model.
Salt: iWk9q-tQgWQTnqDgdoxaXQ==
HMAC-Sha256: b158c5a1bbcdac3cf87fe761030828cb5811b0a6fdfa6366c7bdfddba6391728
HMAC-sha512: e350ca7f0349c2b16a410f224b1ad0c8fc9319708b1dd2be9e83a53b3d4b93d9dd1
f0637ea27641edcfac3d3196795d9889778bd4894ad332ba643d0735aa089
Advanced Encryption Standard (AES)
The national institute of standards and technology (NIST) announced a call for a project for creating a new cipher in January 1997. Many groups had proposed various ciphers. Various ciphers were examined on speed and security parameters and after several rounds of studies and examinations, NIST has finally chosen an algorithm known as Rijndael. Rijndael selected as the best algorithm in terms of security, cost, resilience, integrity and surveillance of the algorithm, hence NIST selected Rijndael as advanced encryption standard (AES) in October 2000.
On 26 November 2001, AES became a FIPS (Federal Information Processing Standards) standard. AES specifies a FIPS-approved cryptographic algorithm used to secure electronic data. The U.S. government (NSA) in June 2003 accepted and announced that AES was secure enough to safeguard highly classified information up to the supersecret level.
Rijndael was named because it was developed by two Belgian cryptographers Dr Joan Daemen and Dr Vincent Rijmen at the Electrical Engineering Department of Katholieke University in Leuven. Rijndael or AES is patent free, and the creators have given out various reference implementations as public domain.
AES Encryption and Decryption in Go
Below sample program will encrypt a text message and decrypt a file using a key, which is basically a 16-byte (128-bit) password. This program will create two files aes.enc which contain encrypted data and aes.key which contains AES key.
This example has a limited use as it is. Use it as a reference for your own applications.
Example
package main
import (
"crypto/aes"
"crypto/cipher"
"crypto/rand"
"encoding/pem"
"fmt"
"io/ioutil"
"log"
)
const (
keyFile = "aes.key"
encryptedFile = "aes.enc"
)
var IV = []byte("1234567812345678")
func readKey(filename string) ([]byte, error) {
key, err := ioutil.ReadFile(filename)
if err != nil {
return key, err
}
block, _ := pem.Decode(key)
return block.Bytes, nil
}
func createKey() []byte {
genkey := make([]byte, 16)
_, err := rand.Read(genkey)
if err != nil {
log.Fatalf("Failed to read new random key: %s", err)
}
return genkey
}
func saveKey(filename string, key []byte) {
block := &pem.Block{
Type: "AES KEY",
Bytes: key,
}
err := ioutil.WriteFile(filename, pem.EncodeToMemory(block), 0644)
if err != nil {
log.Fatalf("Failed in saving key to %s: %s", filename, err)
}
}
func aesKey() []byte {
file := fmt.Sprintf(keyFile)
key, err := readKey(file)
if err != nil {
log.Println("Creating a new AES key")
key = createKey()
saveKey(file, key)
}
return key
}
func createCipher() cipher.Block {
c, err := aes.NewCipher(aesKey())
if err != nil {
log.Fatalf("Failed to create the AES cipher: %s", err)
}
return c
}
func encryption(plainText string) {
bytes := []byte(plainText)
blockCipher := createCipher()
stream := cipher.NewCTR(blockCipher, IV)
stream.XORKeyStream(bytes, bytes)
err := ioutil.WriteFile(fmt.Sprintf(encryptedFile), bytes, 0644)
if err != nil {
log.Fatalf("Writing encryption file: %s", err)
} else {
fmt.Printf("Message encrypted in file: %s\n\n", encryptedFile)
}
}
func decryption() []byte {
bytes, err := ioutil.ReadFile(fmt.Sprintf(encryptedFile))
if err != nil {
log.Fatalf("Reading encrypted file: %s", err)
}
blockCipher := createCipher()
stream := cipher.NewCTR(blockCipher, IV)
stream.XORKeyStream(bytes, bytes)
return bytes
}
func main() {
var plainText = "AES is now being used worldwide for encrypting digital information, including financial, and government data."
encryption(plainText)
fmt.Printf("Decrypted Message: %s", decryption())
}
Output
Message encrypted in file: aes.enc
Decrypted Message: AES is now being used worldwide for encrypting digital inform
ation, including financial, and government data.
High-level design of AES
AES have arithmetic operations are based on Galois Filed which have GF(2N) structure where N = 8. AES is a symmetric cipher which uses the same key for both encryption and decryption process. This symmetric cipher encrypts a 128-bit block of plaintext using a 128-bit key value to produce a 128-bit ciphertext at a time. AES needs a large 128-bit key size to implement encryption and decryption process.
AES 128-bit cipher uses 10 rounds(a substitution and permutation network design with a single collection of steps) of operation for performing encryption and decryption processes. Depending on the types of keys and number of rounds operations, the three versions are AES-128 uses 10 rounds, AES-192 uses 12 rounds and AES-256 uses 14 rounds of operations are in used available.
AES entire data block is being processed in an identical way during each round. In AES, a plaintext has to travel through Nr number of rounds before producing the cipher. Again, each round comprises four different operations. One operation is permutation and the other three are substitutions. They are SubBytes, ShiftRows, MixColumns, and AddRoundKey.
In AES, all the transformations that are being used in the encryption process will have the inverse transformations that are being used in the decryption process. Each round of the decryption process in AES uses the inverse transformations InvSubBytes(), InvShiftRows() and InvMixColumns().
Strong encryption with AES
As AES was produced after DES, all identified attacks on DES have been demonstrated on AES, and all the final results were valid. AES is more confident to brute-force attack than DES because of its larger variable key size and block size. AES is not susceptible to statistical attacks, and it has been tested that it is not achievable with common techniques to do the statistical analysis of ciphertext in AES. As of today, there is no differential, linear and successful attack on AES has been detected. The best part of AES is that the algorithms used in it are so basic that they can be quickly implemented using cheap processors and a minimum amount of memory. AES needs higher processing and more rounds of transmission than DES, and we can comparatively tell this is AES's disadvantage.
Rivest–Shamir–Adleman (RSA)
In 1977, three young scientists Ron Rivest, Adi Shamir, and Leonard Adleman of the Massachusetts Institute of Technology (MIT) took the concept of public-key cryptography and developed an algorithm we called as the RSA algorithm. Using the first letters of their last names, they derived RSA. This algorithm uses public key cryptography (also called asymmetric encryption), so it uses two different keys to encrypt and decrypt data. In RSA, a pair of keys generated where one key revealed to the external world, known as a public key, and the other one kept a secret to the user, known as a private key. They developed this algorithm to address two key issues: create secure communications without having to trust a separate key distribution coordinator with your key and to verify a message comes intact from the claimed sender.
Basic concept of RSA
In asymmetric key cryptography, it generates a pair of keys. The public key is getting published on other hands the private key keep remaining secret. These two keys are numerically linked to each other. Since it generates these keys using a one-way function, it is impossible to generate a private key after knowing the public key, and vice versa. A message encrypted through a key is not practical to decrypt using a similar key. Hence, the secrecy of a message remains secured.
Let us assume that Alice and Bob need to transfer secret messages between themselves using the RSA algorithm. They first generate their proper key sets and publish the public key so that the other body can access it.
The denotations of their public and private keys are as follow :
Public-A and Private-A for Alice
Public-B and Private-B for Bob
When Alice sends a message to Bob, she encrypts the message(M) using Public-B and generates a ciphertext(C) using formula:
C = Public-B(M)
After receiving Cipher-B, Bob can decrypt the message employing his private key, Private-B. This can be formally expressed as:
M = Private-B(C)
Each of the parties keeps his or her private key secret from each other. Consequently, a message that is encrypted using the public key can only be decrypted with its relevant private key.